高斯-博内定理：修订间差异

删除的内容添加的内容

行内

2018年5月30日 (三) 05:23的版本

在微分几何中，高斯-博内定理（亦称高斯-博内公式）是关于曲面的图形（由曲率表征）和拓扑（由欧拉示性数表征）间联系的一项重要表述。它是以卡尔·弗里德里希·高斯和皮埃尔·奥西安·博内命名的，前者发现了定理的一个版本但从未发表，后者1848年发表了该定理的一个特例。

定理内容

设 $M$ 是一个紧的二维黎曼流形， $\partial M$ 是其边界。令 $K$ 为 $M$ 的高斯曲率， $k_{g}$ 为 $\partial M$ 的测地曲率。则有

\int _{M}K\;dA+\int _{\partial M}k_{g}\;ds=2\pi \chi (M),\,

其中dA是该曲面的面积元，ds是M边界的线元。此处 $\chi (M)$ 是 $M$ 的欧拉示性数。

如果 $\partial M$ 的边界是分段光滑的，我们将 $\int _{\partial M}k_{g}\;ds$ 视作光滑部分相应的积分之和，加上光滑部分在曲线边界上的转过的角度之和。

一般化的高斯-博內定理

廣義高斯-博內定理(generalized Gauss–Bonnet theorem)成立於偶數維數的閉黎曼流形。在偶數維數的閉黎曼流形，歐拉示性數仍然可以表達爲曲率多項式的積分。

公式：

$\int _{M}{\mbox{Pf}}(\Omega )=(2\pi )^{n}\chi (M)\$ 。

這是對於高維空間的直接推廣。

例如在四維空間：

$\chi (M)={\frac {1}{32\pi ^{2}}}\int _{M}\left(|Rm|^{2}-4|Rc|^{2}+R^{2}\right)d\mu$

二維高斯-博内定理的操作式證明

由於文獻^[1]^[2]證得微型指南車就是一台能遂行列維-奇維塔向量平行移動的機器(Machine of parallel transport, or parallel-transporter)，今吾人可利用此一特性，操作一台微型指南車，使其純滾動行駛於緊緻定向的二維曲面(黎曼流形)的小區域，且車頭方向永遠保持與行駛路徑相同方向，這就等同於該路徑上的切向量，使得微型指南車平台中央都會劃過曲面路徑的一點，那麼微型指南車平台就恰似該點的切平面，則其車架就相當於一個活動標架，現令此車行駛分段光滑單連通封閉路徑如下圖所示：

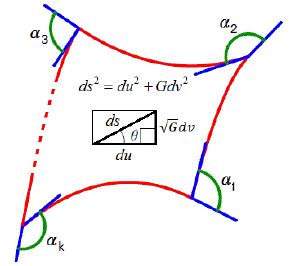
當此車行駛分段光滑封閉路徑回到原出發處且車架回正同剛出發時狀態，那麼由文獻^[3]可證得該微型指南車其指向器之幾何相位方程如下：

\delta =2\pi -\int _{A}K\;dA,\,

其中

\delta =\int _{\partial A}k_{g}\;ds+\sum _{i=1}^{k}\alpha _{i}

上式中的 $\delta$ 定義為微型指南車經歷巡迴路程中指向器的幾何相位，其組成有兩項，全部是由微型指南車所貢獻，一項是微型指南車平移時反應測地曲率而給於指向器的偏轉角，另一項則是微型指南車車頭行駛方向經轉折處時，車頭需要於該點調整拐角的外角和，將此兩項統合起來，就是觀察者乘坐於微型指南車行駛於曲面時，從車架上觀察指向器相對於車頭方向的角度變化，以物理學角度可說 $\delta$ 是在非慣性系觀察所得的指向器偏轉量。

如將前述微型指南車其指向器之幾何相位方程稍作歸整，很容易發現該幾何相位方程就是如下列所示之局部高斯-博内公式(local Gauss -Bonnet formula)^[4]：

2\pi =\int _{A}K\;dA+\int _{\partial A}k_{g}\;ds+\sum _{i=1}^{k}\alpha _{i}

今將此推廣至一個整體緊的二維黎曼流形 $M$ ，令 $\partial M$ 是其邊界，且 $\partial M$ 的邊界是分段光滑的，如果 $K$ 為 $M$ 的高斯曲率， $k_{g}$ 為 $\partial M$ 的測地曲率，那麼就能得到如前頭揭示適用高斯-博內定理的複雜區域和拓撲（由歐拉示性數表徵）間聯繫的一項重要表述，也就是下列式子：

\int _{M}K\;dA+\int _{\partial M}k_{g}\;ds+\sum _{i=1}^{k}\alpha _{i}=2\pi \chi (M),\,

其中

\chi (M)

是

M

的歐拉示性數。

上式中的 $dA$ 是該曲面的面積元， $ds$ 是 $M$ 邊界的線元，式子裡頭的 $k_{g}\;ds$ 積分項是為光滑部分相應測地曲率總和的貢獻，外加上光滑部分在曲線邊界上所有轉過角度之和的貢獻，這在微分幾何專書中例如^[5]^[6]著作裡能找到相關證明。1827年，高斯證明了這一定理。1848年，博內將這一定理推廣到一般曲面上，由任一閉曲線所圍成的單連通區域，形成了前述著名的高斯-博內公式。1944年，陳省身大師給出了高維裡高斯-博內定理的一個內蘊證明^[7]。用指南車，也能給出二維高斯-博内定理的操作式證明^[3]。

特例：指南車定在球面上北緯30度的緯圓轉一圈經高斯-博内定理調控下的操作式實驗證明

在這個例子中，吾人感興趣的只是向量繞某個閉曲線尤其是在球面緯圓作平行移動一周之後，經高斯-博內定理調控下該向量方向或幾何相位的變化。今有一半徑為 $r$ 之球面 $M$ ，則此球面 $M$ 的高斯曲率為 $K=1/r^{2}$ ，那麼在北緯 $\phi$ 到 $\phi +\mathrm {d} \phi$ 的緯圓面積元 $\;dA=2\pi \,r\,\cos {\phi }\,r\,\mathrm {d} \phi$ ，這樣就能求出從特定北緯 $\lambda$ 覆蓋到北極之立體角如下：

\int _{A}K\;dA=\int _{\lambda }^{\pi /2}\,({\frac {1}{r^{2}}})(2\pi \,r\,\cos {\phi }\,r\,\mathrm {d} \phi )=2\pi \,-2\pi \,\sin {\lambda }

將上述式子與局部高斯-博内公式逐項比較，可找出向量於北緯 $\lambda$ 平行移動繞該緯圓一圈後之測地曲率積分項為：

\int _{\partial A}k_{g}\;ds=-2\pi \,\sin {\lambda }

再經前述微型指南車其指向器之幾何相位方程核對上述式子，可發現該式等於微型指南車經歷巡迴路程中指向器的幾何相位 $\delta$ ，進而可以從理論上求得北緯30度緯圓的幾何相位為180度(負號表順時鐘轉)。根據前一節最後得到微型指南車其指向器之幾何相位方程，理論上便知道當如何操作指南車讓指向器能改變一個向量使其作平行移動進而圍繞單連通區域的閉曲線，但在實際情況下往往並不是那麼容易操作的。所幸球面的對稱性與指南車中心相對於兩側雙輪具左右對稱性，只要指南車相對球面是夠小的話，其實這個指南車操作式實驗證明是容易實施的，在本文段落右上方布置了一項實際實驗視訊，正是拿一台指南車置於夠大的地球儀上，且車架中心恆對準北緯30度線，只要穩當操作，讓指南車純滾動行駛一圈之後，可以觀察到指南車上頭的指向器當順時鐘方向轉180度，與前述理論推算值完全吻合。另，這個指南車在球面上的操作式實驗，也能給出傅科擺擺面進動的理論與實驗證明^[3]。雖然佛科擺是一種動態的物理系統，綜合來看，它確實具有物理與幾何更深層的連結，研究 ^[8]^[9]^[10]^[11]指出不同緯度傅科擺擺面週期互異，其擺面一天幾何相位也是： $\delta =-2\pi \,\sin {\lambda }$ 。

參考文獻

^ J. Foster ，J.D. Nightingale，A Short Course in General Relativity，3rd Ed，Springer，2005，Appendex B.
^ M. Santander. The Chinese South-Seeking chariot：A simple mechanical device for visualizing curvature and parallel transport. Am. J. Phys. 1992, 60 (9): 782–787.
^ ^3.0 ^3.1 ^3.2 鄧崇林; 蕭先雄. 指南車在物理學中幾何相位的應用. 物理與工程. 2014, 24 (S2): 1–8. [1]
^ R. Millman, G. Parker, Elements of Differential Geometry. Prentice-Hall, NJ, 1977, pp.185-187.
^ M.P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall, NJ. 1976. pp.274-276.
^ B. O'Neill, Elementary differential geometry, Academic Press, Rev. 2nd ed., 2006. pp.378-383.
^ Shiing-Shen Chern. A Simple Intrinsic Proof of the Gauss-Bonnet Formula for Closed Riemannian Manifolds. Annals of Mathematics. 1944, 45 (4): 747–752. JSTOR 1969302.
^ J. B. Hart; R. E. Miller; and R. L. Mills. A simple geometrical model for visualizing the motion of a Foucault pendulum. Am. J. Phys. 1987, 55 (1): 67–70.
^ J. Oprea. Geometry and the Foucault Pendulum. The American Mathematical Monthly. 1995, 102 (6): 515–522.
^ J. von Bergmann; and H. C. von Bergmann. Foucault pendulum through basic geometry. Am. J. Phy. 2007, 75 (10): 888–892.
^ S. Boersma. A Mathematician's Look at Foucault's Pendulum. Math Horizons. 2005, Feb: 19–21.

外部链接

高斯-博内定理
Spherical Geometry Demo（一個演示球面上切向量沿緯圓平行移動轉一圈時由高斯-博内定理造成的幾何相位轉動變化）

[1] J. Foster ，J.D. Nightingale，A Short Course in General Relativity，3rd Ed，Springer，2005，Appendex B.

[2] M. Santander. The Chinese South-Seeking chariot：A simple mechanical device for visualizing curvature and parallel transport. Am. J. Phys. 1992, 60 (9): 782–787.

[coolteng-3] 3.0 ^3.1 ^3.2 鄧崇林; 蕭先雄. 指南車在物理學中幾何相位的應用. 物理與工程. 2014, 24 (S2): 1–8. [1]

[4] R. Millman, G. Parker, Elements of Differential Geometry. Prentice-Hall, NJ, 1977, pp.185-187.

[5] M.P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall, NJ. 1976. pp.274-276.

[6] B. O'Neill, Elementary differential geometry, Academic Press, Rev. 2nd ed., 2006. pp.378-383.

[7] Shiing-Shen Chern. A Simple Intrinsic Proof of the Gauss-Bonnet Formula for Closed Riemannian Manifolds. Annals of Mathematics. 1944, 45 (4): 747–752. JSTOR 1969302.

[8] J. B. Hart; R. E. Miller; and R. L. Mills. A simple geometrical model for visualizing the motion of a Foucault pendulum. Am. J. Phys. 1987, 55 (1): 67–70.

[9] J. Oprea. Geometry and the Foucault Pendulum. The American Mathematical Monthly. 1995, 102 (6): 515–522.

[10] J. von Bergmann; and H. C. von Bergmann. Foucault pendulum through basic geometry. Am. J. Phy. 2007, 75 (10): 888–892.

[11] S. Boersma. A Mathematician's Look at Foucault's Pendulum. Math Horizons. 2005, Feb: 19–21.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

@@ 第34行： / 第34行： @@
 今將此推廣至一個整體[[緊空間|緊的]]二維[[黎曼流形]]<math>M</math>，令<math>\partial M</math>是其邊界，且<math>\partial M</math>的邊界是[[分段光滑]]的，如果<math>K</math>為<math>M</math>的[[高斯曲率]]，<math>k_g</math>為<math>\partial M</math>的[[測地曲率]]，那麼就能得到如前頭揭示適用'''高斯-博內定理'''的複雜區域和拓撲（由[[歐拉示性數]]  表徵）間聯繫的一項重要表述，也就是下列式子：
 :<math>\int_M K\;dA+\int_{\partial M}k_g\;ds+\sum_{i=1}^{k}\alpha_{i}=2\pi\chi(M), \, </math>  其中 <math>\chi(M)</math>是<math>M</math>的[[歐拉示性數]]。
-上式中的<math>dA</math>是該曲面的面積元，<math>ds</math>是<math>M</math>邊界的線元，式子裡頭的<math>k_g\;ds</math>積分項是為光滑部分相應[[測地曲率]]總和的貢獻，外加上光滑部分在曲線邊界上所有轉過角度之和的貢獻，這在[[微分幾何]]專書中例如<ref>M.P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall, NJ. 1976. pp.274-276.</ref><ref>B. O'Neill, Elementary differential geometry, Academic Press, Rev. 2nd ed., 2006. pp.378-383.</ref>著作裡能找到相關證明。1827年，高斯證明了這一定理。1848年，博內將這一定理推廣到一般曲面上，由任一閉曲線所圍成的單連通區域，形成了前述著名的高斯-博內公式。1944年，[[陳省身]]大師給出了高維裡'''高斯-博內定理'''的一個內蘊證明<ref>{{cite journal|author1=Shiing-Shen Chern|title=A Simple Intrinsic Proof of the Gauss-Bonnet Formula for Closed Riemannian Manifolds|journal=Annals of Mathematics|year=1944|volume=45|issue=4|pages=747–752}}</ref>。用指南車，也能給出二維'''高斯-博内定理'''的操作式證明<ref name="coolteng"/>。
+上式中的<math>dA</math>是該曲面的面積元，<math>ds</math>是<math>M</math>邊界的線元，式子裡頭的<math>k_g\;ds</math>積分項是為光滑部分相應[[測地曲率]]總和的貢獻，外加上光滑部分在曲線邊界上所有轉過角度之和的貢獻，這在[[微分幾何]]專書中例如<ref>M.P. do Carmo, Differential Geometry of Curves and Surfaces, Prentice-Hall, NJ. 1976. pp.274-276.</ref><ref>B. O'Neill, Elementary differential geometry, Academic Press, Rev. 2nd ed., 2006. pp.378-383.</ref>著作裡能找到相關證明。1827年，高斯證明了這一定理。1848年，博內將這一定理推廣到一般曲面上，由任一閉曲線所圍成的單連通區域，形成了前述著名的高斯-博內公式。1944年，[[陳省身]]大師給出了高維裡'''高斯-博內定理'''的一個內蘊證明<ref>{{cite journal|author1=Shiing-Shen Chern|title=A Simple Intrinsic Proof of the Gauss-Bonnet Formula for Closed Riemannian Manifolds|journal=Annals of Mathematics|year=1944|volume=45|issue=4|pages=747–752| jstor=1969302}}</ref>。用指南車，也能給出二維'''高斯-博内定理'''的操作式證明<ref name="coolteng"/>。
 ===特例：指南車定在球面上北緯30度的緯圓轉一圈經高斯-博内定理調控下的操作式實驗證明===
@@ 第42行： / 第42行： @@
 將上述式子與'''局部高斯-博内公式'''逐項比較，可找出向量於北緯<math>\lambda</math>平行移動繞該緯圓一圈後之[[測地曲率]]積分項為：
 :<math>\int_{\partial A}k_g\;ds=-2\pi\,\sin{\lambda}</math>
-再經前述微型指南車其'''指向器之幾何相位方程'''核對上述式子，可發現該式等於微型指南車經歷巡迴路程中指向器的幾何相位 <math>\delta</math>，進而可以從理論上求得北緯30度緯圓的幾何相位為180度(負號表順時鐘轉)。根據前一節最後得到微型指南車其'''指向器之幾何相位方程'''，理論上便知道當如何操作指南車讓'''指向器'''能改變一個向量使其作平行移動進而圍繞單連通區域的閉曲線，但在實際情況下往往並不是那麼容易操作的。所幸球面的對稱性與指南車中心相對於兩側雙輪具左右對稱性，只要指南車相對球面是夠小的話，其實這個指南車操作式實驗證明是容易實施的，在此網頁右上方布置了一項實際實驗視訊，正是拿一台指南車置於夠大的地球儀上，且車架中心恆對準北緯30度線，只要穩當操作，讓指南車純滾動行駛一圈之後，可以觀察到指南車上頭的指向器當順時鐘方向轉180度，與前述理論推算值完全吻合。另，這個指南車在球面上的操作式實驗，也能給出[[傅科擺]]擺面進動的理論與實驗證明<ref name="coolteng"/>。雖然佛科擺是一種動態的物理系統，綜合來看，它確實具有物理與幾何更深層的連結，研究
+再經前述微型指南車其'''指向器之幾何相位方程'''核對上述式子，可發現該式等於微型指南車經歷巡迴路程中指向器的幾何相位 <math>\delta</math>，進而可以從理論上求得北緯30度緯圓的幾何相位為180度(負號表順時鐘轉)。根據前一節最後得到微型指南車其'''指向器之幾何相位方程'''，理論上便知道當如何操作指南車讓'''指向器'''能改變一個向量使其作平行移動進而圍繞單連通區域的閉曲線，但在實際情況下往往並不是那麼容易操作的。所幸球面的對稱性與指南車中心相對於兩側雙輪具左右對稱性，只要指南車相對球面是夠小的話，其實這個指南車操作式實驗證明是容易實施的，在本文段落右上方布置了一項實際實驗視訊，正是拿一台指南車置於夠大的地球儀上，且車架中心恆對準北緯30度線，只要穩當操作，讓指南車純滾動行駛一圈之後，可以觀察到指南車上頭的指向器當順時鐘方向轉180度，與前述理論推算值完全吻合。另，這個指南車在球面上的操作式實驗，也能給出[[傅科擺]]擺面進動的理論與實驗證明<ref name="coolteng"/>。雖然佛科擺是一種動態的物理系統，綜合來看，它確實具有物理與幾何更深層的連結，研究
 <ref>{{cite journal|author1= J. B. Hart|author2= R. E. Miller|author3=and R. L. Mills|title=A simple geometrical model for visualizing the motion of a Foucault pendulum|journal=Am. J. Phys.|year=1987|volume=55|issue= 1|pages=67–70}}</ref><ref>{{cite journal|author1=J. Oprea|title=Geometry and the Foucault Pendulum|journal=The American Mathematical Monthly|year=1995|volume=102|issue=6|pages=515–522}}</ref><ref>{{cite journal|author1=J. von Bergmann|author2=and H. C. von Bergmann|title=Foucault pendulum through basic geometry|journal=Am. J. Phy.|year=2007|volume=75|issue=10|pages=888–892}}</ref><ref>{{cite journal| author1=S. Boersma|title=A Mathematician's Look at Foucault's Pendulum|journal=Math Horizons|year=2005|volume=Feb|pages=19–21}}</ref>指出不同緯度傅科擺擺面週期互異，其擺面一天幾何相位也是：<math>\delta=-2\pi\,\sin{\lambda}</math>。